Impedanţa rezistenţei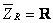

Impedanţa bobinei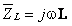

Impedanţa condensatorului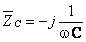

Deoarece aceste 3 impedanţe sunt în serie:

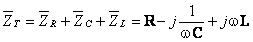, respectiv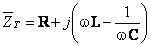

În funcţie de valoarea părţii imaginare a impedanţei, pot exista 3 cazuri:

Cazul 1

Partea imaginară a impedanţei este nulă, 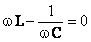, iar impedanţa totală este pur rezistivă, .

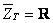Diagrama fazorială a tensiunii de alimentare şi a curentului care parcurge impedanţa totală este de forma:

Faţă de bornele circuitului, acesta are un caracter rezistiv.

 

Cazul 2

Partea imaginară a impedanţei este pozitivă, 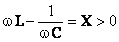, rezultând că impedanţa totală este rezistivă şi inductivă, .

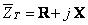Diagrama fazorială a tensiunii de alimentare şi a curentului care parcurge impedanţa totală este de forma:

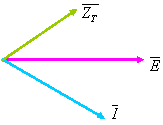
Faţă de bornele circuitului, acesta are un caracter rezistiv şi inductiv.

 

Cazul 3

Partea imaginară a impedanţei este negativă, 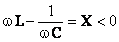, rezultând că impedanţa totală este rezistivă şi capacitivă, .

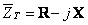Diagrama fazorială a tensiunii de alimentare şi a curentului care parcurge impedanţa totală este de forma:

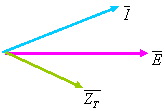
Faţă de bornele circuitului, acesta are un caracter rezistiv şi capacitiv.

Pentru cazul concret al problemei, înlocuind valorile: 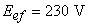, , 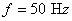, 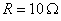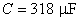şi 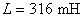, se obţine:

Pentru modulul impedanţei totale

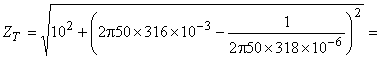
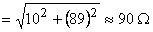
iar pentru faza impedanţei totale

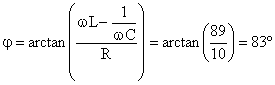
Impedanţa totală compleză va fi deci:

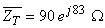
Amplitudinea complexă (valoarea eficace) a curentului este:

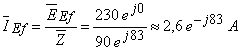
Amplitudinea complexă (valoarea eficace) a tensiunii la bornele rezistenţei este:

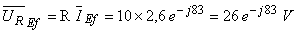
Amplitudinea complexă (valoarea eficace) a tensiunii la bornele inductanţei este:

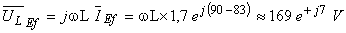
Amplitudinea complexă (valoarea eficace) a tensiunii la bornele condensatorului este:

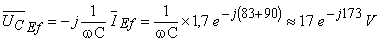
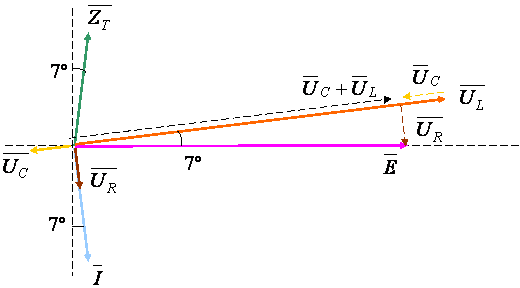
Diagrama fazorială a acestor mărimi este reprezentată în figura următoare, în care se evidenţiază relaţia care există între tensiunile din circuit (Teorema a II-a a lui Kirchhoff)